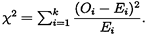ATLAS.TI

Resumen

ATLAS. TI es una herramienta computacional usada como apoyo para el proceso de análisis de contenido (entrevistas, observaciones, documentos impresos, etc.) de la investigación Cualitativa.

Puede trabajar con una gran variedad de información, cuya gama de orígenes, pueden ser textos, observaciones directas, fotografías y datos gráficos, sonoros y audiovisuales.

En  Atlas.ti desarrollamos nuestro proyecto intelectual, llamado Unidad Hermenéutica (UH) al modo de un edificio en el que utilizamos distintas piezas con sus propias cualidades y funciones. 

Elementos de construcción del edificio. Los objetos de Atlas/ti 

v Documentos primarios, documentos en texto (o bien documentos gráficos o sonoros) situados en cualquier parte del disco duro. Permanecen como ficheros independientes. Atlas/ti no los modifica ni los guarda para sí; almacena referencias a ellos, pero el fichero sigue intacto.

v Citas, son fragmentos de los documentos primarios que han sido marcados como tales desde Atlas/ti. Se supone que marcados con alguna finalidad relacionada con su significación. Citas pueden ser una cadena de texto (desde una palabra hasta muchos párrafos) o un área de un gráfico. Las citas nos van a permitir hilar muy fino; si para determinado fin lo que nos interesa es esa frase de ese documento.

v Códigos, son palabras-clave (keywords), indicadores de conceptos o de expresiones que interesan al usuario, por la razón que sea. Los códigos suelen utilizarse para marcar (codificar) determinadas citas.

v Notas (llamadas memos en Atlas/ti), normalmente textos breves que contienen ideas y que se asocian a alguno de los otros tipos de objetos (aunque también pueden no estar asociados). No hay que confundirlas con los comentarios aclaratorios que cualquier objeto puede llevar, dado que las notas a que ahora aludimos tienen entidad propia.

v Familias, un conjunto de objetos que comparten una cualidad. Puede haber familias de códigos, de documentos primarios, etc. Por supuesto, un mismo elemento puede pertenecer a distintas familias. Pueden ser la base de un filtro: en determinados momentos nos interesará restringir una búsqueda a los miembros de tal o cual familia. 

v Vistas de redes, compuestas de nodos y relaciones. Para crear estas redes existe un editor específico. Los nodos pueden ser cualquiera de los objetos antes descritos: desde una cita hasta un código. Las relaciones son los nexos establecidos entre esos nodos y se representarán por flechas de distinto tipo... pero ocurre que de hecho hay distintos tipos de relaciones. Pueden ser del tipo "forma parte de", "apoya a", "contradice a" o como nosotros las definamos.  Hay que diferenciar entre una red y una vista de red. La red es el conjunto de todas las relaciones entre los elementos de un proyecto o UH; la vista de red puede centrarse en sólo una parte de esas relaciones o de esos elementos.

Construcción de un proyecto. Uso de Atlas/ti 

v Crear un proyecto y utilizarlo como "contenedor" de nuestros materiales. Reunimos nuestros documentos primarios y los asignamos a una Unidad Hermenéutica (UH, el nombre que se le da en Atlas/ti a ese proyecto) a la que ponemos un nombre.

v Análisis-Codificación. Analizamos los documentos y vamos marcando en ellos citas, pasajes. Asignamos a estas citas distintos códigos, que pueden estar creados previamente o que podemos ir creando sobre la marcha.

v Notas. Eventualmente, se nos pueden ocurrir ideas que no van pegadas a un documento primario. Las redactamos en forma de nota.

v Teorizar/Interpretar. Se supone que a estas alturas, analizados nuestros datos, hemos ganado mucho en nuestro conocimiento de estos y en la comprensión de los fenómenos y relaciones que subyacen en éstas. A "tejer" esto se le puede llamar trabajo de teorización. Como resultado de esto (o tal vez como ayuda para esto) podemos organizar nuestros objetos en redes.

v Búsquedas. En cualquier momento podemos formular búsquedas a través de todos los componentes de la UH.

Ejemplo

INFOGRAFÍA

MÉTODOS DE INVESTIGACIÓN CIENTÍFICA

SPSS-- DEFINICIONES

INVESTIGACIÓN

TABLAS DE CONTINGENCIA

CHI-CUADRADO

Esta prueba puede utilizarse incluso con datos medibles en una escala nominal. La hipótesis nula de la prueba Chi-cuadrado postula una distribución de probabilidad totalmente especificada como el modelo matemático de la población que ha generado la muestra.

Para realizar este contraste se disponen los datos en una tabla de frecuencias. Para cada valor o intervalo de valores se indica la frecuencia absoluta observada o empírica (Oi). A continuación, y suponiendo que la hipótesis nula es cierta, se calculan para cada valor o intervalo de valores la frecuencia absoluta que cabría esperar o frecuencia esperada (Ei=n·pi , donde n es el tamaño de la muestra y pi la probabilidad del i-ésimo valor o intervalo de valores según la hipótesis nula). El estadístico de prueba se basa en las diferencias entre la Oi y Ei y se define como:

Estudia la relación entre las variables. Se selecciona en el menú estadístico de la tabla de contingencia. La hipótesis nula a contrastar es la independencia de las variables, siendo la dependencia la hipótesis alternativa.

Al pedir el chi cuadrado SPSS nos da su valor, que se calcula al poner en relación los valores observados con los esperados. En nuestro caso la Chi-cuadrado es de 3,157. Esto de por sí solo no nos dice mucho, sin embargo SPSS también nos facilita el nivel de significación que en este caso es de 0,532. Este nivel indica la probabilidad de rechazar la hipótesis nula de independencia siendo cierta. Si esta probabilidad es menor que 0,05 se rechaza la hipótesis nula y en consecuencia diremos que las variables son dependientes entre sí. En nuestro ejemplo, el nivel de significación es de 0,532, por lo que no podemos rechazar la hipótesis nula y decimos que las variables son independientes entre sí, o que no guardan una relación de dependencia.

CORRELACIONES

El concepto de relación o correlación entre dos variables se refiere al grado de parecido o variación conjunta existente entre las mismas. En este apartado vamos a estudiar un tipo particular de relación llamada lineal y se limita a considerar únicamente el caso de dos variables cuantitativas (correlación simple). Una relación lineal positiva entre dos variables X e Y significa que los valores de las dos variables varían de forma parecida: los sujetos que puntúan alto en X tienden a puntuar alto en Y y los que puntúan bajo en X tienden a puntuar bajo en Y. Una relación lineal negativa significa que los valores de ambas variables varían justamente el revés. La forma más directa de formarse una primera idea sobre el tipo de relación existente entre dos variables cuantitativas es a través de un Diagrama de dispersión. Este tipo de diagramas puede obtenerse mediante: Gráficos, en las diferentes opciones que tiene: Generador de Gráficos, Cuadros de diálogo antiguos o en Gráficos interactivos.

Para poder cuantificar el grado de relación lineal existente entre dos variables cuantitativas, así como medir el grado de ajuste de la nube de puntos a una recta, vamos a estudiar coeficientes de correlación. En el procedimiento de Tablas de Contingencia ya se puede obtener el coeficiente de correlación de Pearson. 

El procedimiento Correlaciones que incluye tres opciones:

 (1) Bivariadas, para el estudio de la relación entre dos variables cuantitativas

(2) Parciales, para el estudio de la relación entre dos variables cuantitativas cuando se controla o elimina el efecto de terceras variables  

(3) Distancias, para el estudio de la relación entre dos variables cualesquiera que sea su nivel de medida. 

COEFICIENTE DE INCERTIDUMBRE

Medida de asociación que refleja la reducción proporcional en el error cuando se utilizan los valores de una variable para pronosticar los valores de la otra variable. Por ejemplo, un valor de 0,83 indica que el conocimiento de una variable reduce en un 83% el error al pronosticar los valores de la otra variable. El programa calcula tanto la versión simétrica como la asimétrica del coeficiente de incertidumbre.

 Es una medida semejante a la anterior en cuanto a su concepción de la asociación de las variables, en relación a la capacidad predictiva y las disminución del error de dicha predicción. La diferencia estriba en su cálculo ya que en este caso la expresión de estos coeficientes depende de toda la distribución y no sólo de los valores modales, por lo que sólo toma el valor 0 en casos de total independencia. Ésta es su ventaja respecto a Lambda, pero es más difícil de interpretar. Oscila entre 0 y 1. Su versión asimétrica se interpreta como la proporción de incertidumbre reducida al predecir los valores de una variable a partir de los de la otra; mientras que la versión simétrica se interpreta como la proporción de incertidumbre reducida al predecir los valores de cualquiera de las dos variables mediante la tabla de contingencia.

BIBLIOGRAFIA:

Bausela, E.. (2005). SPSS: UN INSTRUMENTO DE ANÁLISIS DE DATOS CUANTITATIVOS . Revista de Informática Educativa y Medios Audiovisuales , 2 (4), 62-69.

se recupero informacion en:

https://www.uclm.es/profesorado/raulmmartin/Estadistica/PracticasSPSS/CORRELACION_CON_SPSS.pdf

https://rua.ua.es/dspace/bitstream/10045/8139/1/CONTINGENCIA.pdf

AGRUPACIÓN DE DATOS EN SPPS

VIDEO TUTORIAL

Aquí aprenderemos como realizar un agrupación de los datos en el programa SPSS

          

SPSS - ANÁLISIS DE DATOS

ANÁLISIS DE INFORMACIÓN BAJADA DEL INEGI 

empleando el programa SPSS

SURY-SPSS by Sury Moreno Lopez on Scribd

ANÁLISIS CUANTITATIVO -SPSS

Programa SPSS

Conclusión:

Se realizó una encuesta de dos preguntas a 23 alumnos del 7°B de la UNACH, la primera pregunta era: ¿Usas el celular en clases? y la segunda fue ¿cuantos colectivos tomas para llegar a la escuela?.

Al realizar el análisis estadístico de nuestra encuesta con este programa SPSS podemos percatarnos que la mayoría de los alumnos del 7° semestre grupo "B" usan el teléfono en hora de clases, es decir más del 80% de los alumnos usa el celular y solamente un aproximado del 20% no lo usa a la hora de las clases,observamos que la media es des 1.43.

En el análisis de la segunda pregunta  acerca de ¿cuantos colectivos tomas para llegar a la escuela? el resultado fue que cerca del 45% de los alumnos no toman ningún colectivo para trasladarse a la escuela, y cerca del 40% toma un colectivo y el 15% toma dos colectivos para llegar a  la institución, se observó una media de 1.70.

Es importante poder realizar el análisis de los datos ya que nos ayudan a comprender mejor los resultados.

MÉTODOS DE LA INVESTIGACIÓN CIENTÍFICA

Mapa elaborado en GoConqr

Se recuperan los elementos que deben tomarse en cuenta para realizar una investigación científica

MEDIDAS DE TENDENCIA CENTRAL, DISTRIBUCIÓN Y DISPERSIÓN

INVESTIGACIÓN...

Aquí encontraras el texto a cerca de la investigación sobre las medidas de tendencia central, distribución y dispersión.

Medidas de Tendencia Central by Sury Moreno Lopez on Scribd

De forma resumida podrás encontrarlo aquí:

DIAGRAMA DE GANTT

INVESTIGACIÓN...

Diagrama de Gantt by Sury Moreno Lopez on Scribd

CRONOGRAMA DE ACTIVIDADES 

Realizada el Ganttproject  un programa útil para tener un calendario de las actividades a realizar, administra nuestro tiempo y así mismo es un  medio de organización.

ENCUESTA LIKERT

ENCUESTA LIKERT by Sury Moreno Lopez on Scribd

INVESTIGACIÓN "ESTADÍSTICA DESCRIPTIVA"

ESTADÍSTICA DESCRIPTIVA Y SUS CARACTERÍSTICAS

¿Qué es la Estadística Descriptiva? 

La estadística descriptiva es la rama de las Matemáticas que recolecta, presenta y caracteriza un conjunto de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela, temperatura en los meses de verano, etc.) con el fin de describir apropiadamente las diversas características de ese conjunto. Al conjunto de los distintos valores numéricos que adopta un carácter cuantitativo se llama variable estadística. Las variables pueden ser de dos tipos:

 • Variables cualitativas o categóricas: no se pueden medir numéricamente (por ejemplo: nacionalidad, color de la piel, sexo).

 • Variables cuantitativas: tienen valor numérico (edad, precio de un producto, ingresos anuales).  

Las variables también se pueden clasificar en:

 • Variables unidimensionales: sólo recogen información sobre una característica (por ejemplo: edad de los alumnos de una clase). 

• Variables bidimensionales: recogen información sobre dos características de la población (por ejemplo: edad y altura de los alumnos de una clase).

• Variables pluridimensionales: recogen información sobre tres o más características (por ejemplo: edad, altura y peso de los alumnos de una clase). 

Cuando se estudia el comportamiento de una variable hay que distinguir los siguientes conceptos:  
• Individuo: cualquier elemento que porte información sobre el fenómeno que se estudia. Así, si estudiamos la altura de los niños de una clase, cada alumno es un individuo; si se estudia el precio de la vivienda, cada vivienda es un individuo.  
• Población: conjunto de todos los individuos (personas, objetos, animales, etc.) que porten información sobre el fenómeno que se estudia. Por ejemplo, si se estudia el precio de la vivienda en una ciudad, la población será el total de las viviendas de dicha ciudad.  

• Muestra: subconjunto que seleccionado de una población. Por ejemplo, si se estudia el precio de la vivienda de una ciudad, lo normal será no recoger información sobre todas las viviendas de la ciudad (sería una labor muy compleja), sino que se suele seleccionar un subgrupo (muestra) que se entienda que es suficientemente representativo.

DATOS. CLASIFICACIÓN, ORGANIZACIÓN Y CONSTRUCCIÓN DE BLOQUES ESTADÍSTICOS

Los datos son medidas y/o números recopilados a partir de la observación. Los datos pueden concebirse como información numérica necesaria para ayudar a tomar una decisión con más bases en una situación particular. Existen muchos métodos mediante los cuales se pueden obtener datos necesarios. Primero, se puede buscar datos ya publicados por otras fuentes. Segundo, se puede diseñar un experimento. En tercer lugar, se puede conducir un estudio. Cuarto, se pueden hacer observaciones del comportamiento, actitudes u opiniones de los individuos en los que se está interesado. Los datos se pueden clasificar en: • Datos discretos. Son respuestas numéricas que surgen de un proceso de conteo. 
• Datos continuos. Son respuestas numéricas que surgen de un proceso de medición. 

ESCALAS DE MEDICIÓN 
La medición de las variables puede realizarse por medio de cuatro escalas de medición: la nominal, ordinal, de intervalo y de razón. Se utilizan para ayudar en la clasificación de las variables, el diseño de las preguntas para medir variables, e incluso indican el tipo de análisis estadístico apropiado para el tratamiento de los datos.  

Una característica esencial de la medición es la dependencia que tiene de la posibilidad de variación. 

a) Medición Nominal.  

En este nivel de medición se establecen categorías distintivas que no implican un orden específico. Por ejemplo, si la unidad de análisis es un grupo de personas, para clasificarlas se puede establecer la categoría sexo con dos niveles, masculino (M) y femenino (F), los encuestados sólo tienen que señalar su género, no se requiere de un orden real. 

b) Medición Ordinal.  
Se establecen categorías con dos o más niveles que implican un orden inherente entre si. La escala de medición ordinal es cuantitativa porque permite ordenar a los eventos en función de la mayor o menor posesión de un atributo o característica. Por ejemplo, en las instituciones escolares de nivel básico suelen formar por estatura a los estudiantes, se desarrolla un orden cuantitativo pero no suministra medidas de los sujetos. Estas escalas admiten la asignación de números en función de un orden prescrito. Las formas más comunes de variables ordinales son ítems (reactivos) actitudinales estableciendo una serie de niveles que expresan una actitud de acuerdo o desacuerdo con respecto a algún referente. Por ejemplo, ante el reactivo: Pemex debe privatizarse, el respondiente puede marcar su respuesta de acuerdo a las siguientes alternativas:  
__  Totalmente de acuerdo
__  De acuerdo 
__  Indiferente
__  En desacuerdo
__  Totalmente en desacuerdo  

Las anteriores alternativas de respuesta pueden codificarse con números que van del uno al cinco que sugieren un orden preestablecido pero no implican una distancia entre un número y otro.

c) Medición de Intervalo.  
La medición de intervalo posee las características de la medición nominal y ordinal. Establece la distancia entre una medida y otra. La escala de intervalo se aplica a variables continuas pero carece de un punto cero absoluto. El ejemplo más representativo de este tipo de medición es un termómetro, cuando registra cero grados centígrados de temperatura indica el nivel de congelación del agua y cuando registra 100 grados centígrados indica el nivel de ebullición, el punto cero es arbitrario no real, lo que significa que en este punto no hay ausencia de temperatura.   

d) Medición de Razón.  

Una escala de medición de razón incluye las características de los tres anteriores niveles de medición (nominal, ordinal e intervalo). Determina la distancia exacta entre los intervalos de una categoría. Adicionalmente tiene un punto cero absoluto, es decir, en el punto cero no existe la característica o atributo que se mide. Las variables de ingreso, edad, número de hijos, etc. son ejemplos de este tipo de escala. El nivel de medición de razón se aplica tanto a variables continuas como discretas.

TIPOS DE GRÁFICAS  

Una gráfica es la representación de datos, generalmente numéricos, mediante líneas, superficies o símbolos, para ver la relación que esos datos guardan entre sí. Sirven para analizar el comportamiento de un proceso, o un conjunto de elementos o signos que permiten la interpretación de un fenómeno. Las gráficas se pueden agrupar en cinco tipos:

GRÁFICAS DE LÍNEAS  
Gráfica simple de líneas  
Muestran la relación entre dos variables cuantitativas. En el eje horizontal (x) se gráfica la variable independiente en el eje vertical (y). Las marcas de los cuadrantes en los ejes marcan las unidades de medida; las escalas en los ejes pueden ser lineales, logarítmicas o ambas.

Polígono de frecuencias  

Otra forma de representación de uso menos común, y muy parecida a las gráficas de líneas, es el polígono de frecuencias. La diferencia fundamental entre ambas es que en el polígono de frecuencias se añaden dos clases con frecuencias cero: una antes de la primera clase con datos y otra después de la última. El resultado es que se "sujeta" la línea por ambos extremos al eje horizontal y lo que podría ser una línea separada del eje se convierte, junto con éste, en un polígono. 

GRÁFICAS DE BARRAS O HISTOGRAMAS  
Se emplea cuando la variable independiente es categórica. Cada barra sólida, ya sea vertical u horizontal representa un tipo de dato. Cuando es necesario representar divisiones de datos se utiliza un gráfica de barras subdivididas. Los histogramas no muestran frecuencias acumuladas, son preferibles para el tratamiento de datos cuantitativos y la barra con mayor altura representa la mayor frecuencia. La sumatoria de las alturas de las columnas equivale al 100% de los datos.
   
Barras verticales  
En el eje horizontal (o de las abscisas) se representan los intervalos de los datos, marcándose de manera continua las fronteras entre cada uno de éstos. De esta manera, el histograma está compuesto por rectángulos, cuyo número coincide con la cantidad de intervalos considerados, el ancho de la base de cada uno de esos rectángulos es la misma siempre y coincide con las fronteras de los intervalos, y la altura corresponde a la frecuencia de cada intervalo. En este tipo de gráficas es recomendable:  

• El empleo de sombreado o colores facilita la diferenciación de las barras. 
• El punto cero se indica en el eje de ordenadas y se deben establecer las unidades en los ejes. 
• La longitud de los ejes debe ser suficiente para acomodar la extensión de la barra.  

Barras horizontales  
Se parecen mucho a las gráficas de columnas, con la salvedad importante de que la función de los ejes se intercambia y el eje horizontal queda destinado a las frecuencias y el eje vertical a las clases.  

Es muy común que este tipo de gráficos se utilicen para ilustrar el tamaño de una población dividida en estratos como, por ejemplo, son sus edades.

Gráficas de columnas bidimensionales  
Un tipo de gráfico muy parecido al histograma es la gráfica de columnas. Para este tipo de gráfica, elaboradas con rectángulos también, se pide que sus bases sean del mismo ancho y sus alturas equivalentes con las frecuencias. Para este tipo, a diferencia del histograma, no es necesario tener una escala horizontal continua, por lo que los rectángulos (o barras) no tienen que aparecer juntas entre sí. 

Gráficas de columnas tridimensionales  

Existe la posibilidad, y si los recursos lo permiten, de representar gráficos compuestos de una manera "tridimensional", es decir, con gráficos que posean no sólo dos ejes, sino tres; y en los que los rectángulos son sustituidos por prismas de base rectangular (ocasionalmente el software en el mercado permite utilizar prismas cuya base son polígonos regulares de más de cuatro lados, pirámides o cilindros). 

GRÁFICAS CIRCULARES  

Denominadas también gráfica de pastel, se utilizan para mostrar porcentajes y proporciones. El número de elementos comparados dentro de un gráfico circular, no deben ser más de  7, ordenando los segmentos de mayor a menor, iniciando con el más amplio a partir de las 12 como en un reloj. Una manera sencilla de diferenciar los segmentos es sombreándolos con colores contrastantes.
Este tipo de gráficas es muy útil cuando lo que se desea es resaltar las proporciones que representan algunos subconjuntos con respecto al total, es decir, cuando se está usando una escala categórica.

GRÁFICAS DE DISPERSIÓN  

Una gráfica de dispersión tiene dos ejes de valores, mostrando un conjunto de datos numéricos en el eje x y otro en el eje y. Combina estos valores en puntos de datos únicos y los muestra en intervalos uniformes o agrupaciones. Los gráficos de dispersión se utilizan normalmente para mostrar y comparar valores numéricos, como datos científicos, estadísticos y de ingeniería. 

GRÁFICAS DE BURBUJAS  

Un tipo de gráfico similar a las gráficas de dispersión son las gráficas de burbujas, en las cuales se presenta la dispersión de las observaciones de la misma forma pero se le añade la posibilidad de visualizar otra variable representada en el tamaño del punto, pues éstos se convierten en círculos (burbujas) con radios proporcionales a las magnitudes que representan. 

PICTOGRAMAS  
Son gráficos con dibujos alusivos al carácter que se está estudiando y cuyo tamaño es proporcional a las frecuencias que representan. Se emplean para representar diferencias cuantitativas simples entre grupos. Los símbolos utilizados para representar valores idénticos deben ser de igual dimensión.  

Actualmente muchos medios masivos de comunicación utilizan gráficos para ilustrar resultados de alguna investigación. Regularmente se utilizan dibujos llamativos para captar el interés del público.

MEDIDAS DE TENDENCIA CENTRAL 

MEDIA, MEDIANA Y MODA 

Cuando se tiene un grupo de observaciones, se desea describirlo a través de un sólo número. Para tal fin, no se usa el valor más elevado ni el valor más pequeño como único representante, ya que sólo representan los extremos. Una de las propiedades más sobresalientes de la distribución de datos es su tendencia a acumularse hacia el centro de la misma. Esta característica se denomina tendencia central. Las medidas de tendencia central más usuales son: la media aritmética, la mediana y la moda.

MEDIA ARITMÉTICA / PROMEDIO
 La media aritmética de n valores, es igual a la suma de todos ellos dividida entre n. Se denota por x. Cuando los datos tienen más de una frecuencia, para obtener la media aritmética se agrega otra columna a la tabla estadística con el producto de las observaciones y sus frecuencias. 
Las características de la media aritmética son:  
1. Es una medida totalmente numérica o sea sólo puede calcularse en datos de características cuantitativas. 
2. En su cálculo se toman en cuenta todos los valores de la variable. 
3. Es lógica desde el punto de vista algebraico.
4. La media aritmética es altamente afectada por valores extremos. 
5. No puede ser calculada en distribuciones de frecuencia que tengan clases abiertas. 
6. La media aritmética es única, o sea, un conjunto de datos numéricos tiene una y sólo una media aritmética.

MEDIANA
 La mediana es el punto central de una serie de datos ordenados de forma ascendente o descendente. De acuerdo al número de casos o datos, hay dos formas para calcular la mediana: para número impar y para número par:

• Número impar de datos ordenados de menor a mayor o de mayor a menor: la mediana es el valor que queda justo al centro. Ejemplo. Obtener la mediana de los siguientes datos: 4, 7, 1, 9, 2, 5, 6. Solución. Ordenando de forma ascendente: 1, 2, 4, 5, 6, 7, 9. El valor que queda al centro es el 5, porque hay tres datos antes y tres datos después de él, entonces la mediana es 5.

 • Número de datos par: en este caso se busca la media aritmética entre los dos valores centrales.
 Ejemplo. Obtener la mediana de los siguientes datos: -3, 5, 18, 4, 11, -6, 9, 10, -1, 2. 
    Solución. Ordenando de forma ascendente: -6, -3, -1, 2, 4, 5, 9, 10, 11, 18. 
Los valores centrales son 4 y 5. Su media aritmética es: 4+5/2=4.5. En este caso, la mediana de este conjunto no pertenece al conjunto de datos.  

MODA 
La moda de un conjunto de datos numéricos es el valor que más se repite, es decir, el que tiene el mayor número de frecuencias absolutas. La moda puede ser no única e inclusive no existir. 
La moda es una medida de tendencia central muy importante, porque permite planificar, organizar y producir para satisfacer las necesidades de la mayoría.

Ejemplo. Obtener la moda de los siguientes datos: -3, 3, -2, 0, 3, -1, -2, 4, 5, -2, 0, 1.   

Solución. Ordenando de forma ascendente: -3, -2, -2, -2, -1, 0, 0, 1, 3, 3, 4, 5. El valor que más se repite es el -2, por lo tanto ese valor es su moda.

MEDIA PONDERADA  

La media ponderada de un conjunto de valores de una variable x a los que se han asignado, respectivamente.

MEDIA GEOMÉTRICA  
La media geométrica de un conjunto de n 

observaciones es la raíz enésima de su producto.

Las características de la media geométrica son:  

1. Se toman en cuenta todos los valores de la variable. 
2. Es afectada por valores extremos aunque en menor medida que la media aritmética. 
3. Si un dato es cero, su resultado será cero. 
4. No puede ser calculada en distribuciones con clase abiertas. 
5. Es mayormente usada para promediar tasas de intereses anuales, inflación razones y valores que muestren una progresión geométrica (efecto multiplicativo sobre el de los años anteriores). 

MEDIA ARMÓNICA  

La media armónica se define como el recíproco de la media aritmética. 

Las características de la media armónica son:  
1. No se influye por la existencia de determinados valores mucho más grandes que el resto.
2. Presenta cambio sensible a valores mucho más pequeños que el conjunto. 3. No está definida en el caso de la existencia de valores nulos. 

CENTRO DE AMPLITUD  

Es el valor que queda en medio de los valores mínimo y máximo.

MEDIDAS DE DISPERSIÓN 

La dispersión mide que tan alejados están un conjunto de valores respecto a su media aritmética. Así, cuanto menos disperso sea el conjunto, más cerca del valor medio se encontrarán sus valores. Este aspecto es de vital importancia para el estudio de investigaciones. 
Se llaman medidas de dispersión aquellas que permiten retratar la distancia de los valores de la variable a un cierto valor central, o que permiten identificar la concentración de los datos en un cierto sector del recorrido de la variable. Se trata de coeficientes para variables cuantitativas.  

RANGO
 El rango de una distribución es la diferencia entre el valor máximo (M) y el valor mínimo (m) de la variable estadística. Para su cálculo, basta con ordenar los valores de menor a mayor m de M. 

Ejemplo. Si se conoce que el valor promedio de días de espera para obtener una licencia de manejo, es de 5 días en la oficina A, y de 7 días en la oficina B, con esta única información no es posible hacer una elección adecuada. Sin embargo, si se sabe que en la oficina A, el número mínimo de días de espera es de 3 y el máximo de 15, mientras que en la oficina B, los valores son 3 y 8 días respectivamente, se podrá tomar una decisión más adecuada para acudir a obtener la licencia, gracias a esta información adicional.  

Características del rango: 
1. A medida que el rango es menor, el grado de representatividad de los valores centrales se incrementa. 
2. A medida que el rango es mayor, la distribución está menos concentrada o más dispersa. 
3. Su cálculo es extremadamente sencillo. 
4. Tiene gran aplicación en procesos de control de calidad. 
5. Tiene el inconveniente de que sólo depende de los valores extremos. De esta forma basta que uno de ellos se separe mucho para que el recorrido se vea sensiblemente afectado. 

MEDIDAS DE POSICIÓN PARA DATOS AGRUPADOS Y NO AGRUPADOS: PERCENTILES, DECILES Y CUARTILES 

Los cuantiles son los valores de la distribución que la dividen en partes iguales, es decir, en intervalos que comprenden el mismo número de valores. Cuando la distribución contiene un número alto de intervalos o de marcas y se requiere obtener un promedio de una parte de ella. Generalmente, se divide la distribución en cuatro, en diez o en cien partes. Los cuantiles más usados son los percentiles, cuando dividen la distribución en cien partes, los deciles, cuando dividen la distribución en diez partes y los cuartiles, cuando dividen la distribución en cuatro partes.

PERCENTILES
Los percentiles son números que dividen en 100 partes iguales un conjunto de datos ordenados. Es decir, El percentil k es un valor que deja aproximadamente el k por ciento de los datos por abajo de él. Se denota por medio de P(k%). 

Ejemplo. En un estudio de ingresos mensuales de la población económicamente activa, revela que el percentil 90 (P90) es $20,000. Esto significa que aproximadamente el 90% de las personas tienen ingresos que son menores o iguales a $20,000, y por supuesto, el 10% tiene ingresos mayores o iguales a dicho valor.

En el ejemplo anterior se tomo el percentil 90 pero se podría haber considerado cualquier valor, por ejemplo, 70, 80 entre otros. Fundamentalmente cuando la distribución de frecuencia es asimétrica, puede ser más útil e informativo, resumir la distribución de la variable en estudio, mediante los percentiles.  

DECILES
 Los deciles son números que dividen la sucesión de datos ordenados en diez partes porcentualmente iguales. Son los nueve valores que dividen al conjunto de datos ordenados en diez partes iguales, son también un caso particular de los percentiles. Los deciles se denotan D(1), D(2),..., D(9), que se leen primer decil, segundo decil, etc. 

CUARTILES  

Los cuartiles se definen como los tres valores que dividen la distribución en cuatro partes iguales. 



RANGO INTERCUARTIL  

Para un cálculo de rangos más eficiente, se eliminan los valores extremadamente alejados aplicando el rango intercuartil que es una medida de variabilidad adecuada cuando la medida de posición central empleada ha sido la mediana y él se define como la diferencia entre el Tercer Cuartil superior y el Primer Cuartil, es decir: Rango Intercuartil = Q(3) – Q(1).
Ejemplo. Dados los siguientes valores ordenados:  
26, 33, 36, 39, 40, 40, (41), 42, 44, 45, 47, 47, 47, (48), 50, 51, 51, 53, 54, 54, (55), 57, 59, 61, 63, 66, 71. 
Obtener su rango y su rango intercuartil.
Solución. El rango es: 71 – 26 = 45 
Los valores cuartiles se muestran entre paréntesis, es decir, 41, 48 y 55, donde, el segundo cuartil es simplemente la mediana. La dispersión calculada a través del rango intercuartil, es en este caso será: Q3 – Q1= 55 - 41 = 14. Nótese como el la dispersión es mucho menor aplicando el rango intercuartil

DESVIACIÓN MEDIA  

La desviación media es la división de la sumatoria del valor absoluto de las distancias existentes entre cada dato y su media aritmética y el número total de datos.
Este indicador muestra que tan disperso se encuentran un conjunto de datos a un punto de concentración.
Ejemplo. Sean los siguientes datos: 4, 5, 3, 5, 3, 2, 2, 2, 2, 3, 5, 1, 4, 1, 4. Obtener su desviación media.
Solución. 

Se calcula la media aritmética:
El primer dato (4), se aleja de la media en 0,9334 hacia la derecha. Para el segundo dato (5), se aleja de la media 1,9333 también hacia la derecha. Para el tercer dato (3), se aleja de la media en 0,0667 pero hacia la izquierda. La suma de las distancias absolutas es 17.2, así que los datos se separan de la media en: 17.2/15=1.1466

DESVIACIÓN ESTÁNDAR  

La desviación estándar o desviación típica se define como la raíz cuadrada de los cuadrados de las desviaciones de los valores de la variable respecto a su media.
La desviación estándar es una medida estadística de la dispersión de un grupo o población. Una gran desviación estándar indica que la población esta muy dispersa respecto de la media. Una desviación estándar pequeña indica que la población está muy compacta alrededor de la media.

VARIANZA  

La varianza mide la mayor o menor dispersión de los valores de la variable respecto a la media aritmética. Cuanto mayor sea la varianza mayor dispersión existirá y por tanto, menor representatividad tendrá la media aritmética. La varianza se expresa en las mismas unidades que la variable analizada, pero elevadas al cuadrado.
La varianza de un conjunto de datos se define como el cuadrado de la desviación estándar y está dada por:  v=O2.

COEFICIENTE DE VARIACIÓN  

Cuando se quiere comparar el grado de dispersión de dos distribuciones que no vienen dadas en las mismas unidades o que las medias no son iguales se utiliza el coeficiente de variación de Pearson que se define como el cociente entre la desviación estándar y el valor absoluto de la media aritmética.
Este coeficiente, representa el porcentaje que la desviación estándar contiene a la media aritmética y por lo tanto cuanto mayor es CV mayor es la dispersión y menor la representatividad de la media. 

ANÁLISIS DESCRIPTIVO DE DATOS BIVARIADOS. CORRELACIÓN  

Hasta ahora se han estudiado los índices y representaciones de una sola variable por individuo. Son del tipo distribución unidimensional.  

Cuando sobre una población se estudian simultáneamente los valores de dos variables estadísticas, el conjunto de los pares de valores correspondientes a cada individuo se denomina distribución bidimensional.

DIAGRAMAS DE DISPERSIÓN  

La distribución conjunta de dos variables puede expresarse gráficamente mediante un diagrama de dispersión: en un plano se representa cada elemento observado haciendo que sus coordenadas sobre los ejes cartesianos sean los valores que toman las dos variables para esa observación.
Se representa la variable dependiente en el eje de las ordenadas y la independiente en el eje de las abscisas. Cuando se estudia la relación entre dos variables, una puede considerarse causa y la otra resultado o efecto de la primera, siendo ésta una decisión teórica. Se conoce como variable exógena, o variable independiente a la que causa el efecto y variable endógena, o variable dependiente a la que lo recibe.
Por supuesto que diferentes conjuntos de datos ofrecerán diagramas diferentes. Sin embargo, se pueden considerar cuatros tipos de diagramas de dispersión, que son los más típicos:  
1. Relación tal que al aumentar los valores de la variable independiente aumenta (en promedio) el valor de la variable dependiente. Cuando esto ocurre hay una relación lineal positiva. 
2. Relación tal que al aumentar los valores de la variable independiente se reduce (en promedio) el valor de la variable dependiente. Cuando esto ocurre hay una relación lineal negativa.
3. No hay relación entre ambas variables. Esto significa que las variables son independientes. 
4. Relación entre ambas, pero no lineal.  

COVARIANZA  
La covarianza es una medida de la asociación lineal entre dos variables que resume la información existente en un gráfico de dispersión. 
Esta medida, refleja la relación lineal que existe entre dos variables. El resultado numérico fluctúa entre los rangos de [ ] ∞∞− , . Al no tener unos límites establecidos no puede determinarse el grado de relación lineal que existe entre las dos variables, sólo es posible ver la tendencia.  

• Una covarianza positiva significa que existe una relación lineal positiva entre las dos variables. Es decir, los valores bajos de la variable x se asocian con los valores bajos de la variable y , mientras los valores altos de x se asocian con los valores altos de la variable y .
 • Una covarianza de negativa significa que existe una relación lineal inversa (negativa) entre las dos variables. Lo que significa que los valores bajos en x se asocian con los valores altos en y , mientras los valores altos en x se asocian con los valores bajos en y . 
• Una covarianza de cero se interpreta como la no existencia de una relación lineal entre las dos variables estudiadas. 

CORRELACIÓN  

Es frecuente que se estudie sobre una misma población los valores de dos variables estadísticas distintas, con el fin de ver si existe alguna relación entre ellas, es decir, si los cambios en una de ellas influyen en los valores de la otra. Si ocurre esto se dice que las variables están correlacionadas o bien que hay correlación entre ellas.
La correlación indica la fuerza y la dirección de una relación lineal entre dos variables aleatorias. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: si se tienen dos variables ( x y y ) existe correlación si al aumentar los valores de x lo hacen también los de y y viceversa. La correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad.

La relación entre dos variables cuantitativas queda representada mediante la línea de mejor ajuste, trazada a partir de la nube de puntos. Los tres principales componentes elementales de una línea de ajuste y, por lo tanto, de una correlación, son la fuerza, el sentido y la forma:  
1. La fuerza mide el grado en que la línea representa a la nube de puntos: si la nube es estrecha y alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos tiene una tendencia elíptica o circular, la relación es débil.  
2. El sentido mide la variación de los valores de y con respecto a x: si al crecer los valores de x lo hacen los de y , la relación es positiva; si al crecer los valores de x disminuyen los de y , la relación es negativa.  

3. La forma establece el tipo de línea que define el mejor ajuste: la línea recta, cuadrática, polinomial, etc.

Funciones Estadísticas de Excel

CONTAR: Esta función cuenta el número de celdas que contienen números en un rango específico. Omite las celdas que contengan texto, así como las que estén vacías. 

CONTAR.SI: Esta función cuenta el número de celdas de un rango específico que cumplen con una condición dada.

COVAR: Calcula la covarianza entre dos conjuntos de datos.

DESVEST: Calcula la desviación estándar de una muestra sin tener en cuenta los valores lógicos y celdas que contengan texto. 

DESVESTA: Esta función también calcula la desviación estándar de una muestra, pero a diferencia de DESVEST, DESVESTA si tiene en cuenta los valores lógicos como VERDADERO (a los que les asigna valores de 1) y FALSO (a los que les asigna valores de 0).

DESVESTP: Calcula la desviación estándar de la población sin tener en cuenta valores lógicos ni texto. 

DESVESTPA: Calcula la desviación estándar de la población total teniendo en cuenta valores lógicos y el texto como VERDADERO a los que se les asigna valor de 1 y FALSO a los que se les asigna 0.

DESVPROM: Calcula el promedio de las desviaciones absolutas de los datos de una muestra a partir de la media.

ESTIMACIÓN.LINEAL: Es una función que se utiliza para estimar los principales estadísticos de una regresión lineal, pendientes, coeficiente de determinación, estadístico F, etc.

ESTIMACION.LOGARITMICA: Es una función que se utiliza para estimar los principales estadísticos de una regresión exponencial, pendientes, coeficiente de determinación, estadístico F, etc.

FRECUENCIA : Esta función calcula la frecuencia, o número de veces, que unos valores se repiten en un intervalo determinado. Estos valores pertenecen a un rango de datos. Como resultado Excel le devuelve una matriz (más bien un vector columna) donde se encuentra la distribución de frecuencia de los datos dadas unas especificaciones de los intervalos. 

INTERSECCION.EJE: Esta función calcula el punto de intersección con el eje Y de una función de X óptima a partir de unos valores de Y (variable dependiente) conocidos y unos valores de X (variable independiente). Esta función óptima la calcula Excel utilizando el método de Estimación Lineal (mínimos cuadrados).  

JERARQUÍA :Esta función muestra la jerarquía o posición de un valor en un conjunto de valores que pueden estar ordenados de forma ascendente o descendente.

K.ESTIMO.MAYOR: Esta función se muestra el valor del valor k-ésimo valor mayor de una matriz de valores, sin importar sus dimensiones.

K.ESTIMO.MENOR: Esta función es vez de mostrar el mayor valor de una matriz determinada muestra el menor.

MAX: Esta función muestra el valor máximo de una o varias matrices (Excel tiene capacidad de hasta 255 matrices). En caso de que la matriz sea de 1x1 ésta será un número tal como lo pide Excel. 
Para saber cuál es el valor máximo se da clic en la celda que se desee mostrar. Luego insertar función, estadísticas MAX y aceptar. 

MAXA: Esta función devuelve el mayor valor de una matriz o varias. Esta función se diferencia de la anterior (MAX) en que estas matrices pueden incluir valores lógico como VERDADERO y FALSO. Para Excel la palabra VERDADERO tiene una equivalencia de 1 y FALSO 0. 

MEDIA.ACOTADA: Esta función calcula la media de un vector (columna o fila) de datos eliminando un porcentaje de estos que se encuentran en los extremos, es decir, los mayores e inferiores sin que estos estén ordénanos (ni de forma ascendente ni descendente).

MEDIA.ARMO: Por medio de esta función Excel calcula la media armónica de una o varias matrices (como máximo 255) cuyos elementos sean mayores a cero.

MEDIANA: Esta función calcula la mediana (valor intermedio de un conjunto de valores, es decir, el que se encuentra en la mitad. No necesariamente debe pertenecer a alguna de las matrices) de los valores de una o varias matrices (máximo 255).

MIN :Esta función calcula el valor mínimo de una o varias matrices (máximo de 255).

MINA: Esta función devuelve el menor valor de una matriz o varias (hasta 255). Esta función se diferencia a la anterior en que estas matrices pueden incluir valores lógico como VERDADERO y FALSO. Para Excel la palabra VERDADERO tiene una equivalencia de 1 y FALSO 0. 

MODA: Esta función calcula la moda (valor que se repite con más frecuencia o número de veces) de una o varias matrices (máximo 255). A partir de este criterio Excel calcula moda de un conjunto de datos formado por una o más matrices. 

PERCENTIL: Esta función de Excel permite calcular el k-ésimo percentil de un conjunto de valores a partir del valor del percentil (%).

PROBABILIDAD: Esta función calcula la probabilidad de que unos valores de un determinado rango se encuentren en un intervalo. 

PROMEDIO: Con esta función Excel calcula el promedio o media aritmética de los elementos de una o varias matrices (hasta 255), sin importar que las dimensiones de éstas sea diferente.

PROMEDIO.SI: Esta calcula lo mismo que la anterior a diferencia que ésta sólo calcula el promedio de una única matriz a partir de una condición (criterio). Este criterio también está en una matriz que debe tener las mismas dimensiones que la matriz a la que se le piensa calcular el promedio.  

Referencia: 

González A. F.(2006). Estadística Descriptiva. Métodos Estadísticos Aplicados a las Auditorías Sociolaborales. Universidad de Cádiz.

Unidad Técnica del Centro de Formación y Desarrollo. (2012). Programa de capacitación y actualización del personal administrativo: Microsoft Excel 2007. México